Modul BDR Matematika ! Menentukan Dua Bangun Sebangun atau Tidak Materi Kesebangunan Kelas 9

Indikator :

• 3.6.4  Mengidentifikasi dua benda sebangun atau tidak. 
• 3.6.5  Menjelaskan syarat-syarat/sifat-sifat dua bangun segi banyak yang sebangun.

Dua bangun datar yang mempunyai bentuk yang sama disebut Sebangun. Tidak perlu ukurannya sama, tetapi sisi-sisi yang bersesuaian sebanding (proportional) dan sudut-sudut yang bersesuaian sama besar. Perubahan bangun satu menjadi bangun lain yang sebangun melibatkan perbesaran atau pengecilan. Dengan kata lain dua bangun dikatakan sebangun jika memenuhi syarat:

(i) perbandingan panjang sisi yang bersesuaian senilai

(ii) sudut yang bersesuaian besarnya sama

Jika bangun ABCD dan EFGH memenuhi kedua syarat tersebut, maka bangun ABCD dan EFGH Sebangun, dinotasikan dengan ABCD 〜 EFGH. Jika bangun ABCD dan EFGH tidak memenuhi kedua syarat tersebut maka bangun ABCD dan EFGH Tidak Sebangun, dinotasikan dengan ABCD ≁ EFGH.

Perhatikan gambar di bawah ini.

Manakah pasangan persegi panjang yang sebangun? Jelaskan.

Periksa sudut-sudut yang bersesuaian. Ketiga gambar tersebut adalah persegi panjang, maka besar setiap sudutnya adalah 90^o. Sehingga, sudut-sudut yang bersesuaian pasti sama besar yaitu 90^o.

Periksa perbandingan sisi-sisi yang bersesuaian:

- Persegi panjang (i) dan (ii)

Diperoleh bahwa perbandingan sisi-sisi yang bersesuaian tidak sama. Jadi, persegi panjang (i) dan (ii) tidak sebangun.

- Persegi panjang (i) dan (iii)

Tampak bahwa perbandingan sisi-sisi yang bersesuaian tidak sama. Jadi, persegi panjang (i) dan (iii) tidak sebangun.

- Persegi panjang (ii) dan (iii)

Tampak bahwa perbandingan sisi-sisi yang bersesuaian senilai. Jadi, persegi panjang (ii) dan (iii) sebangun. Ingat: EFGH sebangun dengan JKLI, tetapi EFGH tidak sebangun dengan IJKL Jadi, pasangan persegi panjang yang sebangun adalah persegi panjang (ii) dan (iii).

Selesaikan soal-soal di bawah ini dengan benar dan sistematis.

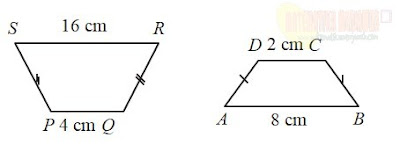
1. Selidikilah apakah dua trapesium di bawah ini sebangun? Jelaskan.

2. Carilah pasangan bangun yang sebangun di antara gambar di bawah ini.