Kunci Jawaban Uji Kompetensi 2 Bab Persamaan dan Fungsi Kuadrat Kelas 9 K13
Uji kompetensi 2 merupakan bagian akhir dari Bab Persamaan dan Fungsi Kuadrat yang terdapat dalam Buku Matematika Kelas 9 Kurikulum 2013 Revisi 2018.
Uji kompetensi 2 ini terdapat pada halaman 129 - 132. Pada bagian ini mengujikan 2 pokok besar materi yaitu Persamaan kuadrat dan Fungsi kuadrat.
Uji kompetensi 2 ini berupa soal uraian. Terdiri dari 30 nomor soal yang
menantang. Namun untuk pembahasan kunci jawabannya akan dibahas secara
bertahap supaya artikel ini tidak menjadi sangat panjang. Pembahasan kali ini
dari nomor 1 sampai dengan 15. Pembahasan nomor selanjutnya akan disampaikan
pada artikel berikutnya.
Soal Uji Kompetensi 2 Bab Persamaan dan Fungsi Kuadrat Kelas 9 K13 [Nomor 1 - 15]
1. Jika p dan q adalah akar-akar persamaan x2 − 5x − 1 = 0,
tentukan persamaan kuadrat baru yang akar-akarnya 2p + 1 dan 2q + 1.
2. Diketahui akar-akar persamaan kuadrat 2x2 – 4x + 1 = 0
adalah m dan n. Tentukan persamaan kuadrat baru yang akar-akarnya m + n dan
m.n.
3. Persamaan 2x2 + qx + (q – 1) = 0 mempunyai akar-akar
x1 dan x2 . Jika x12 + x22 = 4, tentukan nilai q!
4. Persamaan(1 – m)x2 + (8 – 2m)x + 12 = 0 mempunyai akar
kembar. Berapa m?
5. Jika nilai diskriminan persamaan kuadrat 2x2 – 9x + c = 0
adalah 121, tentukan nilai c.
6. Jumlah dua bilangan cacah adalah 12. Jika hasil kali dua bilangan
itu 35, tentukan kedua bilangan cacah yang dimaksud.
7. Persamaan kuadrat x2 − 2x + 7 = 0 mempunyai akar-akar
x1 dan x2 . Persamaan kuadrat yang akar-akarnya x1
− 2 dan x2 – 2 adalah ....
8. Akar-akar persamaan 2x2 − 6x + 2m − 1 = 0 adalah dan . Jika = 2, maka nilai m adalah ....
9. Jika p dan q adalah akar-akar persamaan x2 − 5x − 1 = 0,
maka persamaan kuadrat
baru yang akar-akarnya 2p + 1 dan 2q + 1 adalah ....
10. Akar-akar persamaan kuadrat x2 + (a − 1)x + 2 = 0 adalah dan . Jika = 2 dan a > 0, tentukan nilai a.
11. Gambarkan grafik fungsi kuadrat berikut.
a. f(x) = x2 + x + 3
b. f(x) = x2 – 6x + 8
c. f(x) = 2x2 + 3x + 2
12. Tentukan fungsi kuadrat yang grafiknya memotong sumbu-x pada titik
koordinat (–2, 0) dan (5, 0) serta memotong sumbu-y pada titik koordinat (0,
–20).
13. Tentukan fungsi kuadrat yang grafiknya memiliki titik puncak pada
titik koordinat (1, 5) serta melalui titik koordinat (0, 7).
14. Tentukan fungsi kuadrat yang grafiknya melalui titik koordinat (0,
5), (1, 6) dan (–1, 12).
15. Tentukan fungsi kuadrat yang grafiknya melalui titik koordinat (0,
–2) serta memiliki sumbu simetri x = –½.
Kunci Jawaban Uji Kompetensi 2 Bab Persamaan dan Fungsi Kuadrat Kelas 9 K13 [Nomor 1 - 15]
Jawaban Soal Nomor 1
Jika p dan q adalah akar-akar persamaan x2 − 5x − 1 = 0,
tentukan persamaan kuadrat baru yang akar-akarnya 2p + 1 dan 2q + 1.
Penyelesaian:
a = 1, b = -5, dan c = -1
p + q = -b/a = -(-5/1) = 5
pq = c/a = -1/1 = -1
x1 + x2 =
(2p + 1) + (2q + 1) = 2(p + q) + 2 = 2 ×
5 + 2 = 12
x1 . x2= (2p
+ 1)(2q + 1) = 4pq + 2(p + q) + 1 = 4(–1) +
2(5) + 1 = 7
Jadi persamaan kuadrat yang baru adalah :
x2 - (x1 + x2)x + x1.x2
= 0
x2 - (12)x + 7 = 0
x2 - 12x + 7 = 0
Jawaban Soal Nomor 2
Diketahui akar-akar persamaan kuadrat 2x2 – 4x + 1 = 0 adalah m
dan n. Tentukan persamaan kuadrat baru yang akar-akarnya m + n dan m .
n !
Penyelesaian:
a = 2 ; b = -4 ; c = 1
Hasil jumlah dan perkalian akar-akar dari persamaan kuadrat lama adalah :
m + n = -b/a = -(-4)/2 = 2
m × n = c/a = 1/2
Hasil jumlah dan perkalian akar-akar dari persamaan kuadrat baru adalah :
x1 + x2 = (m + n) + (m.n) = 2 + 1/2 = 5/2
x1 . x2 = (m + n) . (m.n) = 2 x 1/2 = 1
Jadi persamaan kuadrat baru yang terbentuk adalah :
x2 - (x1 + x2)x + x1.x2
= 0
x2 - (5/2)x + 1 = 0
x2 - 5/2x + 1 = 0
Jawaban Soal Nomor 3
Persamaan 2x2 + qx + (q – 1) = 0 mempunyai akar-akar x1
dan x2. Jika x12+ x22 = 4, tentukan nilai q!
Penyelesaian:
x1 + x2 = -b/a = -q/2
x1x2 = c/a = (q-1)/2
Sehingga:
x12 + x22 = 4 ⇔ (x1 + x2)2 –
2x1x2 = 4 ⇔ (-q/2)2 - 2(q-1/2) = 4
q2/4 − q + 1 = 4 ⇔ q2 - 4q + 4 = 16 ⇔ q2 – 4q – 12 = 0 ⇔ (q + 2)(q – 6) = 0
⇔ q = –2 atau q = 6
Jawaban Soal Nomor 4
Persamaan (1 – m)x2 + (8 – 2m)x + 12 = 0 mempunyai akar
kembar. Berapa m?
Penyelesaian:
a = 1 - m ; b = 8 - 2m ; c = 12
Akar kembar jika nilai diskriminan (D) nol.
Sehingga:
D = 0 ⇔ b2 - 4ac = 0 ⇔ (8 – 2m)2 – 4(1 – m)(12) = 0 ⇔ 64 – 32m + 4m2
– 48 + 48m = 0
⇔ 16 + 16m + 4m2 = 0 ⇔ m2 + 4m + 4 = 0 ⇔ (m + 2)2 = 8 ⇔ m =
–2 ±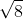 
Jawaban Soal Nomor 5
Jika nilai diskriminan persamaan kuadrat 2x2 – 9x + c = 0
adalah 121, tentukan nilai c.
Penyelesaian:
a = 2 ; b = -9 ; c = c
Nilai D Persamaan kuadrat adalah 121 sehingga:
D = 121 ⇔ b2 - 4ac = 121 ⇔ (–9)2 – 4(2)(c) = 121 ⇔ 81 – 8c = 121 ⇔ 8c = –40 ⇔ c
= –5
Jawaban Soal Nomor 6
Jumlah dua bilangan cacah adalah 12. Jika hasil kali dua bilangan itu
35, tentukan kedua bilangan cacah yang dimaksud.
Penyelesaian:
Misal dua bilangan cacah tersebut adalah a dan b
Dengan demikian maka a + b = 12 ⇔ a = 12 – b dan ab = 35
Diperoleh:
ab = 35 ⇔ (12 – b)b = 35 ⇔ 12b – b2 – 35 = 0 ⇔ b2
– 12b + 35 = 0 ⇔ (b – 7)(b – 5) = 0 ⇔ b = 7 atau b = 5
Untuk b = 7 diperoleh a = 12 – 7 = 5
Untuk b = 5 diperoleh a = 12 – 5 = 7
Jadi kedua bilangan cacah tersebut adalah 5 dan 7
Jawaban Soal Nomor 7
Persamaan kuadrat x2 −2x + 7 = 0 mempunyai akar-akar x1 dan x2.
Persamaan kuadrat yang akar-akarnya x1 − 2 dan x2– 2 adalah ....
Penyelesaian:
a = 1 ; b = -2 ; c = 7
Hasil jumlah dan kali akar-akar persamaan kuadrat lama:
x1 + x2 = -b/a = -(-2)/1 = 2
x1.x2 = c/a = 7/1 = 7
Hasil jumlah dan kali akar-akar persamaan kuadrat baru:
x1 + x2 = (x1 – 2) + (x2 – 2) = x1 + x2 – 4 = 2 – 4 = –2
x1.x2 = (x1 – 2) + (x2 – 2) = x1.x2 – 2(x1 + x2) + 4 = 7 – 2(2) + 4 = 7
Jadi persamaan kuadrat yang baru adalah:
x2 - (x1 + x2)x + x1.x2 = 0
x2 - (-2)x + 7 = 0
x2 + 2x + 7 = 0
Jawaban Soal Nomor 8
Akar-akar persamaan 2x2 − 6x + 2m − 1 = 0 adalah α dan β .
Jika α = 2β, maka nilai m adalah ....
Penyelesaian:
a = 2 ; b = -6 ; c = 2m - 1
α + β = -(-6)/2 ⇔ α + β = 3
Oleh karena α = 2β maka 2β + β = 3 ⇔ β = 1 dan α = 2 sehingga :
αβ = c/a ⇔ 2 x 1 = (2m − 1) / 2 ⇔
2 = (2m − 1) / 2 ⇔ 2m – 1 = 4 ⇔ 2m = 5 ⇔ m = 5/2
Jawaban Soal Nomor 9
Jika p dan q adalah akar-akar persamaan x2 − 5x − 1 = 0,
tentukan persamaan kuadrat baru yang akar-akarnya 2p + 1 dan 2q + 1.
Penyelesaian:
a = 1, b = -5, dan c = -1
p + q = -b/a = -(-5/1) = 5
pq = c/a = -1/1 = -1
x1 + x2 = (2p + 1) + (2q + 1) =
2(p + q) + 2 = 2 × 5 + 2 = 12
x1 . x2= (2p + 1)(2q + 1) = 4pq +
2(p + q) + 1 = 4(–1) + 2(5) + 1 = 7
Jadi persamaan kuadrat yang baru adalah :
x2 - (x1 + x2)x + x1.x2 = 0
x2 - (12)x + 7 = 0
x2 - 12x + 7 = 0
Jawaban Soal Nomor 10
Akar-akar persamaan kuadrat x2 + (a − 1)x + 2 = 0 adalah α dan β. Jika α =
2β dan a > 0, tentukan nilai a.
Penyelesaian: αβ = c/a ⇔ αβ = 2 ⇔ 1/2 α2 = 2 ⇔ α2 = 4 ⇔ α = 2 dan β = 1. Didapatkan:
α + β = a – 1 ⇔ 3 = a – 1 ⇔ a = 4
Jawaban Soal Nomor 11
11. Gambarkan grafik fungsi kuadrat berikut.
a. f(x) = x2 + x + 3
b. f(x) = x2 – 6x + 8
c. f(x) = 2x2 + 3x + 2
Jawaban Soal Nomor 12
12. Tentukan fungsi kuadrat yang grafiknya memotong sumbu-x pada
koordinat (–2, 0) dan (5, 0) serta memotong sumbu-y pada titik koordinat
(0, –20).
Penyelesaian:
Bentuk umum fungsi kuadrat: f(x) = y = ax2 + bx + c
# grafiknya memotong sumbu-x pada koordinat (–2, 0) maka a(-2)2 + b(-2)
+ c = 0. Diperoleh 4a - 2b + c = 0
# grafiknya memotong sumbu-x pada koordinat (5, 0) maka a(5)2 + b(5) + c
= 0. Diperoleh 25a + 5b + c = 0
# grafiknya memotong sumbu-y pada titik koordinat (0, –20) maka -20 =
a(0)2 + b(0) + c. Diperoleh c = -20
Dari ketiga persamaan di atas maka dengan mengeliminasi b:
25a + 5b + -20 = 0 , persamaan dikalikan 2 maka menjadi 50a + 10b - 40
= 0
4a - 2b + -20 = 0 , persamaan dikalikan 5 maka menjadi 20a - 10b -
100 = 0
Kedua persamaan dijumlahkan sehingga diperoleh:
50a + 20a + 10b + (-10b) - 40 + (-100) = 0
70a - 140 = 0
70a = 140
a = 140/70 = 2
Selanjutnya mencari nilai b
50a + 10b - 40 = 0 ⇔ 50.2 + 10b - 40 = 0 ⇔ 100 + 10b - 40 = 0 ⇔ 10b + 60
= 0 ⇔ 10b = -60 ⇔ b = -60/10 = -6
Dengan a = 2 ; b = -6 dan c = -20 maka fungsi kuadrat dari grafik adalah
f(x) = 2x2 – 6x – 20
Jawaban Soal Nomor 13
13. Tentukan fungsi kuadrat yang grafiknya memiliki titik puncak pada
titik koordinat (1, 5) serta melalui titik koordinat (0, 7).
Penyelesaian:
# grafik melalui titik koordinat (0, 7) maka y = ax2 +bx + c a(0)2
+b(0) + c = 7 c = 7
# titik puncak (titik ekstrim) grafik = (xp,yp) = (-b/2a, D/-4a) = (1,
5)
xp = -b/2a ⇔ -b/2a = 1 ⇔ 2a = -b ⇔ 2a + b = 0
yp = D/-4a ⇔ b2 - 4ac / -4a = 5 ⇔ b2 - 4ac = -20a ⇔ b2 - 4a.7 = -20a ⇔
b2 - 28a = -20a ⇔ b2 -8a = 0
2a + b = 0 ⇔ a = -b/2 , masukkan persamaan ini ke persamaan b2 - 8a = 0
sehingga:
b2 - 8a = 0
b2 - 8 (-b/2) = 0
b2 + 4b = 0
b (b + 4) = 0
b = 0 atau b = -4
b = 0 maka a = 0/2 = 0 , tidak memenuhi karena nilai a dalam fungsi
kuadrat tidak boleh 0.
b = -4 maka a = -(-4)/2 = 2
Dengan a = 2 ; b = -4 dan c = 7 maka fungsi kuadrat dari grafik tersebut
adalah f(x) = 2x2 – 4x + 7
Jawaban Soal Nomor 14
14. Tentukan fungsi kuadrat yang grafiknya melalui titik koordinat (0,
5), (1, 6) dan (–1, 12).
Penyelesaian:
# grafik melalui titik koordinat (0, 5) maka a(0)2 +b(0) + c = 5 ⇔ c =
5
# grafiknya melalui titik koordinat (1, 6) maka a(1)2 + b(1) + c = 6 ⇔ a
+ b + c = 6
# grafiknya melalui titik koordinat (–1, 12) maka a(-1)2 + b(-1) + c =
12 ⇔ a - b + c = 12
Karena c = 5 maka a + b + c = 6 menjadi a + b + 5 = 6 ⇔ a + b = 1
Karena c = 5 maka a - b + c = 12 menjadi a - b + 5 = 12 ⇔ a - b = 7
Eliminasi b untuk memperoleh nilai a dengan menjumlahkan kedua
persamaan,
a + b = 1
a - b = 7
Diperoleh,
a + a + b - b = 1 + 7 ⇔ 2a = 8 ⇔ a = 8/2 = 4
Selanjutnya mencari nilai b
dengan a = 4 maka a + b = 1 menjadi 4 + b = 1 ⇔ b = -3
Dengan a = 4 ; b = -3 ; dan c = 5 maka fungsi kuadrat dari grafik adalah
f(x) = 4x2 – 3x + 5
Jawaban Soal Nomor 15
Tentukan fungsi kuadrat yang grafiknya melalui titik koordinat (0, –2)
serta memiliki sumbu simetri x = –½
Penyelesaian: f(x) = 1/3x2 + 1/3x – 2
Demikian Kunci Jawaban Uji Kompetensi 2 Bab Persamaan dan Fungsi Kuadrat
Kelas 9 K13. Semoga bermanfaat.
You might like :
- Kunci Jawaban Uji Kompetensi 1 Bab Perpangkatan dan Bentuk Akar Kelas 9 K13 [Nomor 1 - 15]
![Kunci Jawaban Uji Kompetensi 1 Bab Perpangkatan dan Bentuk Akar Kelas 9 K13 [Nomor 1 - 15]](https://blogger.googleusercontent.com/img/b/R29vZ2xl/AVvXsEiBJm_O4w536-jyetVHpZOHCwMZAuvfisf0YkJO7uewdew3xIgHQgMTHtD87kQmn2y2uNuUiAuyMVOuiBAllJl_ww9B8JsMGZCGbgi76UnmCZML0WdMVhsmGFTsTl5Bnd5k5_modPYfwy9m/w191-h123-p-k-no-nu/soal+nomor+11.jpg "Kunci Jawaban Uji Kompetensi 1 Bab Perpangkatan dan Bentuk Akar Kelas 9 K13 [Nomor 1 - 15]")
- Bank Soal Kelas 9 Bab Peluang untuk UN SMP 2020
- Kompetensi Dasar, Indikator, dan Tujuan Pembelajaran Bab Kekongruenan dan Kesebangunan Kurikulum 2013 Revisi 2018
- Menggambar Sketsa Grafik Fungsi Kuadrat Dengan Contoh Soal Dan Pembahasannya
- Kompetensi Dasar, Indikator, dan Tujuan Pembelajaran Bab Transformasi Kurikulum 2013 Revisi 2018
- Modul BDR Matematika ! Menentukan Dua Benda Kongruen atau Tidak Kongruen Kelas 9
- Kompetensi Dasar, Indikator, dan Tujuan Pembelajaran Bab Perpangkatan dan Bentuk Akar Kurikulum 2013 Revisi 2018
- Kompetensi Dasar, Indikator, dan Tujuan Pembelajaran Bab Persamaan dan Fungsi Kuadrat Kurikulum 2013 Revisi 2018
Ditunggu komentarnya gaess !