Persamaan Sumbu Simetri Dan Titik Optimum Grafik Fungsi Kuadrat Dengan Contoh Soal Dan Pembahasannya

Hai apa kabar? Masih semangat mempelajari tentang fungsi kuadrat? Pelajaran kali ini melanjutkan materi sebelumnya. Pada pertemuan lalu kita sudah belajar tentang pengertian fungsi kuadrat dan karakteristik grafik fungsi kuadrat.

Pertemuan kali ini kita akan belajar tentang persamaan sumbu simetri dan titik optimum dengan tujuan sebagai berikut:

• Mengidentifikasi sumbu simetri dari grafik fungsi kuadrat f(x) dengan memperhatikan nilai dari koefisien x² dan x.
• Menentukan nilai optimum dari fungsi kuadrat.

Pelajaran ini akan diawali dengan penjelasan materi yang diikuti dengan contoh soal. Pada bagian akhir ada soal-soal latihan sebagai latihan pemantapan materi. Mari belajar!

Perhatikan gambar!

Sumbu simetri grafik fungsi kuadrat merupakan sebuah garis yang membagi kurva menjadi 2 bagian sama besar

Sumbu simetri biasanya digambarkan dengan garis putus-putus seperti tampak pada gambar di atas.

Sumbu simetri grafik fungsi kuadrat ditentukan oleh persamaan :

Perhatikan gambar!

Titik optimum disebut juga titik puncak dan disebut juga titik balik.

Titip optimum terdiri dari titik optimum maksimum dan titik optimum minimum.

Titik optimum maksimum terjadi jika grafik terbuka ke bawah. Sedangkan titik optimum minimum terjadi jika grafik terbuka ke atas.

Titik optimum (xp,yp) = (,  )

Nilai yp disebut nilai optimum.

Serupa dengan penjelasan di atas maka nilai yp dapat berupa nilai maksimum atau nilai minimum.

Baik nilai minimum atau nilai maksimum ditentukan dengan rumus yang sama yaitu 

Contoh 1

1. Tentukan sumbu simetri dari fungsi kuadrat berikut!

a. y = x²

b. y = -x² + 3x

c. y = 2x² + 2x  - 5

d. y = - 1/4 x² – 4x - 1

Penyelesaian

a. y = x² → a = 1; b = 0

x= -b/2a = - 0/2.1 = 0/2 = 0

Jadi sumbu simetri grafik y = x² adalah x = 0

b. y = -x² + 3x → a = -1; b = 3

x= -b/2a = - 3/(2.(-1)) = 3/2 =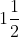

Jadi sumbu simetri grafik y = -x² + 3x adalah x =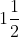

c. y = 2x² + 2x  - 5 → a = ........ ; b = ...........

x= -b/2a = - (………..)/(2.……..) = (…………)/(…………) = .............

Jadi sumbu simetri grafik y = 2x² + 2x  - 5 adalah x =  ..............

d. y = - 1/4 x² – 4x – 1 → a = 1; b = 0

x= -b/2a = - (………..)/(2.……..) = (…………)/(…………) = .............

Jadi sumbu simetri grafik y = - 1/4 x² – 4x – 1 adalah x = ...............

Contoh 2

Tentukan titik puncak (titik optimum) dari y = x² - 1!

Penyelesaian

a = 1 , b = 0, c = -1

Xp =  -b/2a = -0/2.1 = -0/2 = 0

Yp = -D/4a = -(b² - 4ac)/4a = -(0²  - 4.1.(-1))/4.1 = -4/4 = -1

Jadi titik puncak dari grafik y = x² – 1 adalah (xp,yp) = (0,-1)

Contoh 3

Tentukan nilai maksimum/minimum dari fungsi y = x² – 2x - 8!

Penyelesaian

a = 1, b = -2, c = -8

a = 1 > 0 (positif) maka grafik fungsi terbuka ke atas

Oleh karena a > 0 maka grafik fungsi memiliki nilai minimum

Y minimum = -D/4a = -(b² - 4ac)/4a = -((-2)²  - 4.1.(-8))/4.1 = -36/4 = -9

Jadi nilai minimum dari grafik fungsi y = x² – 2x – 8 adalah -9.

Petunjuk : Kerjakan soal-soal berikut sesuai contoh yang telah diberikan di atas.

1. Tentukan sumbu simetri dari fungsi kuadrat berikut!

2. Tentukan sumbu simetri dari fungsi kuadrat y = 1/2 x² !

3. Tentukan titik puncak (titik optimum) dari!

4. Tentukan nilai maksimum/minimum dari fungsi y = x² – 3x + 2!