Menggambar Sketsa Grafik Fungsi Kuadrat Dengan Contoh Soal Dan Pembahasannya

Saria Bakti 19 September, 2020 Tidak ada komentar

Hai apa kabar? Masih semangat mempelajari tentang fungsi kuadrat? Pelajaran kali ini melanjutkan materi sebelumnya. Pada pertemuan lalu kita sudah belajar tentang persamaan sumbu simetri dan titik optimum grafik fungsi kuadrat.

Pertemuan kali ini kita akan belajar tentang Menggambar Sketsa Grafik Fungsi Kuadrat dengan tujuan sebagai berikut:

Menjelaskan hubungan antara nilai diskriminan dan titik potong grafik fungsi kuadrat terhadap sumbu-x.
Membuat sketsa grafik fungsi kuadrat.

Menggambar Sketsa Grafik Fungsi Kuadrat Dengan Contoh Soal Dan Pembahasannya

Pelajaran ini akan diawali dengan penjelasan materi yang diikuti dengan contoh soal. Pada bagian akhir ada soal-soal latihan sebagai latihan pemantapan materi. Mari belajar!

Pendalaman Materi Menggambar Sketsa Grafik Fungsi Kuadrat

Selain menggunakan tabel koordinat (x,y), sketsa grafik fungsi kuadrat juga dapat dibuat dengan memperhatikan karakteristik grafik fungsi kuadrat seperti sumbu simetri, titik optimum, titik potong terhadap sumbu-x dan titik potong terhadap sumbu-y.

Lebih jelasnya berikut langkah-langkah menggambar grafik fungsi kuadrat.

1. Tentukan bentuk parabola (terbuka ke atas atau ke bawah)

a > 0 (positif) maka grafik y = ax² + bx + c akan terbuka ke atas dan memiliki titik puncak minimum
a < 0 (negatif) maka grafik y = ax² + bx + c akan terbuka ke bawah dan memiliki titik puncak maksimum.

2. Tentukan titik potong grafik terhadap sumbu x → y = 0.

3. Tentukan titik potong grafik terhadap sumbu y → x = 0.

4. Menentukan sumbu simetri

Persamaan sumbu simetri → 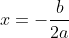$x = -\frac{b}{2a}$

5. Menentukan titik puncak (titik optimum).

Titik puncak → (xp, yp) = ( $-\frac{b}{2a}$ , $-\frac{D}{4a}$ )

6. Sketsakan grafik

DISKRIMINAN PADA FUNGSI KUADRAT

Karakteristik grafik berdasarkan nilai diskriminan:

Jika D > 0 maka grafik akan memotong sumbu x pada dua titik.
Jika D = 0 maka grafik akan memotong sumbu x pada satu titik (menyinggung sumbu x).
Jika D < 0 maka grafik tidak memotong sumbu x.

Lebih jelasnya perhatikan gambar di atas!

Contoh 1

Tentukan apakah grafik y = x² - 2x – 8 memotong sumbu x atau tidak!

Penyelesaian

a = 1, b = -2, c = -8

D = b² - 4ac = (-2)² - 4(1)(-8) = 4 + 32 = 36

Jadi oleh karena D > 0 artinya grafik memotong sumbu x pada dua titik.

Contoh 2

Gambarkan Sketsa grafik fungsi kuadrat y = x² - 2x - 8!

Penyelesaian

Menetukan bentuk parabola

a = 1 > 0 (positif) artinya grafik terbuka ke atas.

Menentukan Titik Potong Grafik Serhadap Sumbu X

Titik potong grafik terhadap sumbu x maka y = 0

y = 0

x² - 2x - 8 = 0

(x - 4)(x + 2) = 0 → diselesaikan dengan cara pemfaktoran (baca tentang pemfaktoran pada persamaan kuadrat)

x = 4 atau x = -2

Jadi, diperoleh titik potong dengan sumbu x adalah (4, 0) dan (-2, 0).

Menentukan Titik Potong Grafik Terhadap Sumbu Y

Titik potong grafik terhadap sumbu y maka x = 0

y = x² - 2x - 8

y = 0² – 2.0 - 8 → ganti x dengan 0

y = - 8

Jadi, titik potong grafik dengan sumbu y adalah (0, -8).

Menentukan Sumbu Simetri

Sumbu simetri grafik = x = -b/2a = -((-2))/2.1 = -((-2))/2 = 1

Menentukan Titik Puncak

Titik puncak grafik adalah (xp,yp) = (-b/2a , -D/4a )

xp = -b/2a = -((-2))/2.1 = -((-2))/2 = 1

yp = -D/4a = -(b² - 4ac)/4a = -(0² - 4.1.(-1))/4.1 = -4/4 = -1

Jadi, koordinat titk puncaknya adalah (1, – 9).

Sketsa Grafik

Hubungkan titik-titik yang diperoleh yang meliputi : (1) titik potong terhadap sumbu x, (2) titik potong terhadap sumbu y, dan (3) titik puncak sehingga menjadi kurva mulus berbentuk parabola seperti terlihat pada gambar berikut.